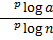IPENDIDIKAN.com - Adik-adik tercinta, kali ini kita belajar tentang pengertian logaritma & operasi aljabar pada bentuk logaritma serta contoh soalnya agar mempermudah adik-adik untuk memahaminya. Jangan lupa berdo'a dulu ya....
Check it out....
Definisi logaritma:
Sampai disini, sudah paham belum dik?
kalau masih bingung dibaca lagi ya.... kalau sudah paham.. lanjutkan !
Dengan n, p, a, & b positif serta n
1 & p1.
Penyelesaian:
3 log 4 + log 18 - log 72
= log 43 + log 18 - log 72
= log 64 + log 18 - log 72
= log
= log 16
= log 24
= 4 log 2
2. Hitunglah nilai logaritma berikut,3log 36 . 6log 81 !
Penyelesaian:
3log 36 . 6log 81
=
= 6log 36 . 3log 81
=6log 62 . 3log 34
= 2 . 4 = 8
Mudah bukan?
Cukup sampai disini ya, pembahasan kali ini..
Terima kasih & Sampai jumpa kembali adik-adik. Salam, Tim iPendidikan.
Check it out....
A. Pengertian Logaritma.
Logaritma adalah kebalikan dari operasi perpangkatan, yaitu mencari pangkat dari suatu bilangan pokok sehingga hasilnya sesuai dengan yang telah diketahui, seperti 32 = 9 diperoleh bahwa 2 merupakan logaritma 9 dengan bilangan pokok 3, & ditulis 2 = 3log 9.Definisi logaritma:
Untuk a dan b positif serta aKeterangan:1 berlaku an = b <---> alog b = n.
- a disebut bilangan pokok, a > 0 & a1. Apabila a = 10, 10log x dapat ditulis log x.
- b disebut numerus, b > 0.
- n adalah hasil dari logaritma.
Contoh Soal.
1. Tentukanlah nilai logaritma
!
Penyelesaian:
= x
jadi,= 6
2. Nyataan bentuk eksponen berikut ini ke notasi logaritma, 34 = 81 !
Penyelesaian:
34 = 81 <---> 3log 81 = 4
3. Nyatakan bentuk logaritma berikut ini ke bentuk berpangkatan, 7log 49 = 2 !
Penyelesaian;
7log 49 = 2 <---> 72 = 49. !Penyelesaian:
= xjadi,
= 62. Nyataan bentuk eksponen berikut ini ke notasi logaritma, 34 = 81 !
Penyelesaian:
34 = 81 <---> 3log 81 = 4
3. Nyatakan bentuk logaritma berikut ini ke bentuk berpangkatan, 7log 49 = 2 !
Penyelesaian;
Sampai disini, sudah paham belum dik?
kalau masih bingung dibaca lagi ya.... kalau sudah paham.. lanjutkan !
B. Operasi Aljabar pada Bentuk Logaritma.
Berikut ini merupakan sifat-sifat logaritma yang dipakai dalam operasi aljabar bentuk logaritma & juga untuk menyederhanakannya.
a. nlog ab = nlog a + nlog b
b. nlog= nlog a - nlog b
c. nlog ap= p nlog a
d. nlog a =
e. nnlog a = a
1 & p1.Contoh Soal.
1. Sederhanakanlah, 3 log 4 + log 18 - log 72 !Penyelesaian:
3 log 4 + log 18 - log 72
= log 43 + log 18 - log 72
= log 64 + log 18 - log 72
= log
= log 16
= log 24
= 4 log 2
2. Hitunglah nilai logaritma berikut,3log 36 . 6log 81 !
Penyelesaian:
3log 36 . 6log 81
=
= 6log 36 . 3log 81
=6log 62 . 3log 34
= 2 . 4 = 8
Mudah bukan?
Cukup sampai disini ya, pembahasan kali ini..
Terima kasih & Sampai jumpa kembali adik-adik. Salam, Tim iPendidikan.